Attention is ALL you need

算法流程

Attention是Transformer结构的核心组成部分，在此对self-attention进行介绍和分析

Self-Attention的算法流程很简单清晰，简单概括：定义三个变换QKV，然后用QK计算每个token的score，与V加权即可

1. 定义三个线性变换

class SelfAttention(nn.module):

  # 定义三个基本的矩阵线性变换QKV
	self.query = nn.Linear(128, 128)  # 假设输入和输出都是128
	self.key = nn.Linear(128, 128)  # 
	self.value = nn.Linear(128, 128)  # 

2. 对同一个句子，假设单个句子的Embedding为(10, 128)，代表一句话10个单词，每个单词128维向量表征，对这个Embedding分别进行QKV三个变换，维度从(10, 128)*(128, 128) = (10, 128)

class SelfAttention(nn.module):

  # 定义三个基本的矩阵线性变换QKV
	self.query = nn.Linear(128, 128)  # 假设输入和输出都是128
	self.key = nn.Linear(128, 128)  # 
	self.value = nn.Linear(128, 128)  # 

	def forward(self, embeddings):
		Q = self.query(embeddings)   # (L, 128)*(128, 128) = (L, 128)
		K = self.key(embeddings)
		V = self.value(embeddings)

3. 根据attention的公式

$Attention(Q, K, V) = softmax(\frac{Q^{T}K}{\sqrt{d_k}})V$

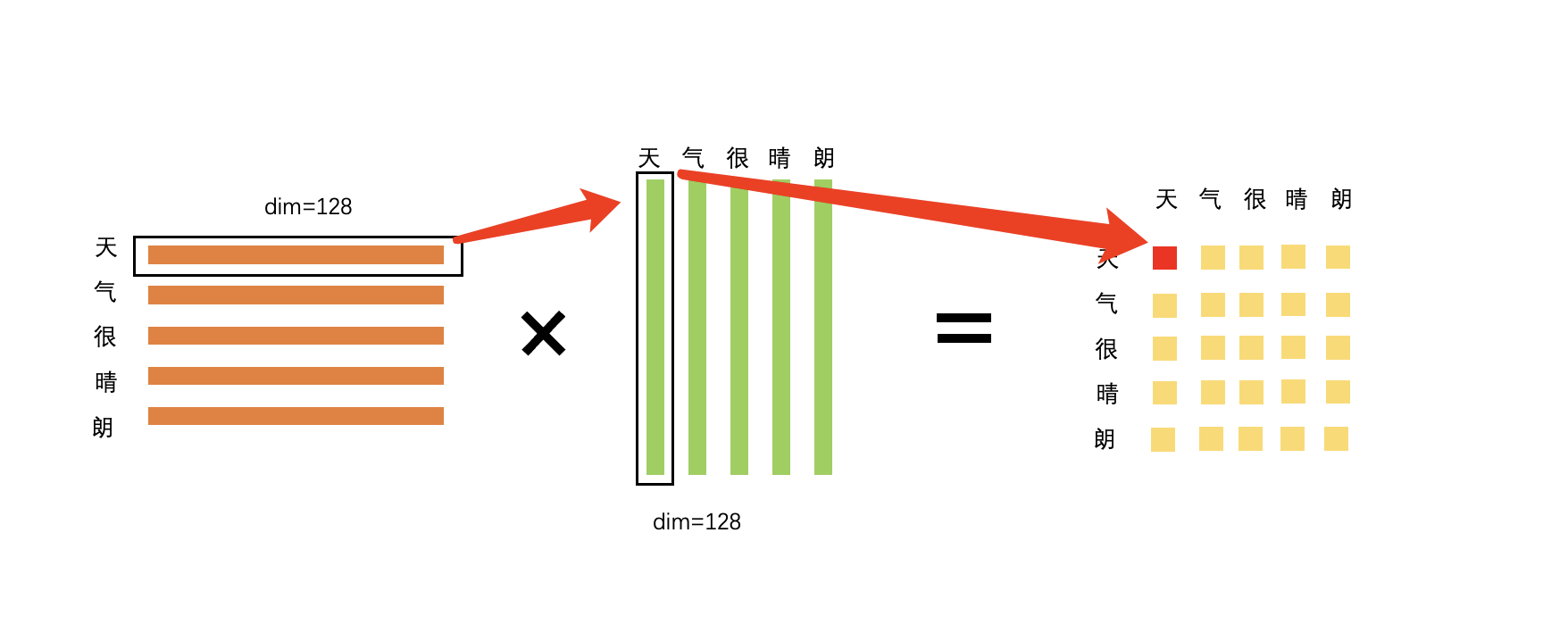
$Q$和$K$相乘，在维度上(L, 128) * (L, 128)^T = (L, L) 本质上**相当于计算了Q中每个token对K中每个token的相似度！**也就是说，attention的是利用token之间的相似度来定义的；之后对其进行$\sqrt{d_k}$的缩放，然后进行softmax归一化，也就是每个$Q$中的token对$K$中的全部token的attention score之和为1，同时增加了非线性；

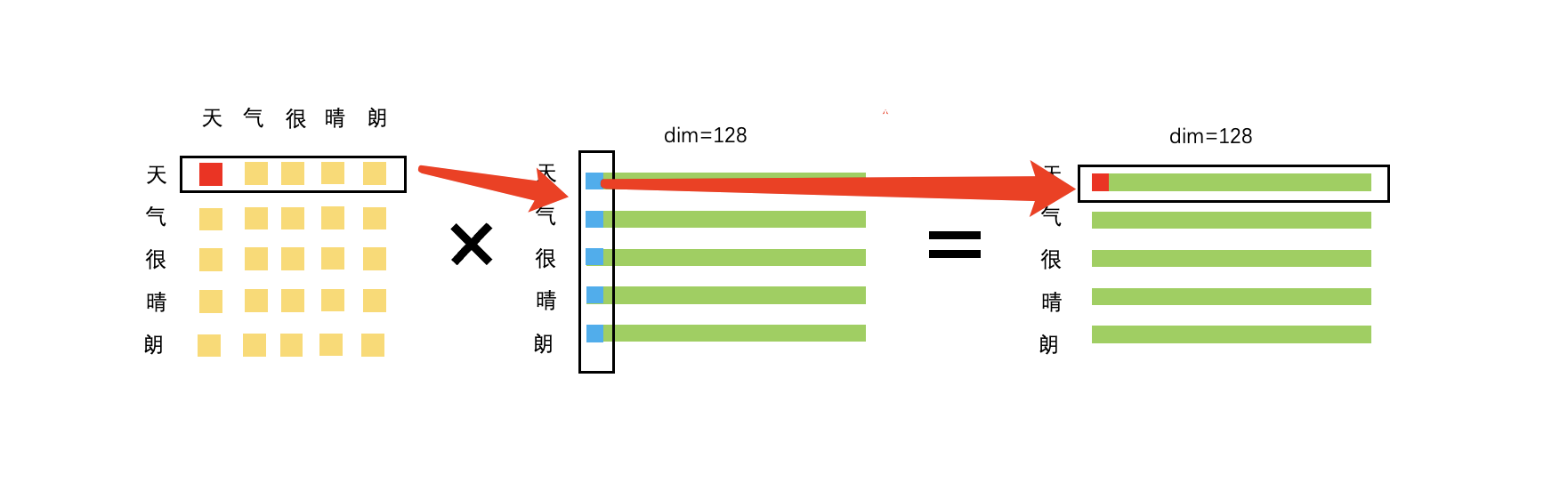
最后attention score与$V$相乘，得到最终结果

class SelfAttention(nn.module):
		self.query = nn.Linear(128, 128)  # 
		self.key = nn.Linear(128, 128)
		self.value = nn.Linear(128, 128)
		self.softmax = nn.Softmax(dim=-1)

		def forward(self, embeddings):
			q = self.query(embeddings)  # (10, 128)
			k = self.key(embeddings)    # (10, 128)
			v = self.value(embeddings)  # (10, 128)
			attention_scores = torch.matmul(Q, K.t())  # (10, 10) 
            attention_scores = attention_scores / math.sqrt(self.attention_head_size)
			attention_probs = self.softmax(attention_scores)
			out = torch.matmul(attention_probs, v)  # (10, 128)
			return out

几点注意

1. 可以看出，如果调换一句话中两个字的位置，实际上在计算attention的时候是没有影响的，也就是attention本质上不考虑位置信息(Textcnn、LSTM这种都有位置信息)，在Bert中是用position embedding来引入位置信息
2. 因为QKV都是从一个句子本身得到，所以叫self-attention
3. 为什么要在softmax之前scaled?向量的点积会很大，因为如果不进行scaled，值过大，进行softmax后的梯度趋于0，会发生梯度消失(已经过实验验证)
4. 为什么用维度$d_k$来放缩？因为假设q和k是均值为0，方差为1互相独立的随机变量，那么q*k的均值是0，方差是$d_k$(可由公式推导得到)，方差越大说明点积可能取到很大，因此很自然的方法就是将方差稳定到1，因此除以$d_k$

References

[1]. Attention Is All You Need